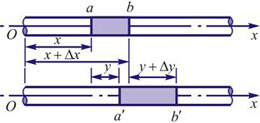
设有截面为$S $、密度为$\rho $的固体细长棒。假定有平面纵波沿着棒长方向传播,棒中的每一小段将不断地受到拉伸和压缩。观察一个体积元$ab $,其原长度为$\Delta x $,体积为$\Delta V$,如果在某一时刻这体积元正在被拉长,左端面处的胁强为$\sigma (=\frac{F}{S}) $(受力方向左),右端面的胁强将为$\sigma +\frac{\partial \sigma}{\partial x}\Delta x$(受力方向向右),式中的$\frac{\partial\sigma}{\partial x}$表示这时刻胁强随距离的改变率。因此体积元所受到的合力
$$
F=-\sigma S+(\sigma+\frac{\partial \sigma}{\partial x}\Delta x)S=\frac{\partial \sigma}{\partial x}S\Delta x\tag1
$$
由牛顿第二定律$F=ma$得到
$$
\frac{\partial \sigma}{\partial x}S\Delta x=\rho S \Delta x \frac{\partial u}{\partial t}\tag2
$$
$$
亦即\frac{\partial \sigma}{\partial x}=\rho \frac{\partial u}{\partial t}\tag3
$$
设体积元左端位移为$y$,右端位移为$y+\Delta y $ .因此体积元的长度变换为$\Delta y$,其原长为$\Delta x$,结合杨氏模量的定义:
$$
E=\frac{\sigma}{\Delta x /x _0}\tag4
$$
立即可以得到
$$
E=\frac{\sigma}{\frac{\partial y}{\partial x}}\tag5
$$
$$
\sigma=E \frac{\partial y}{\partial x}=E\underset{\Delta x \rightarrow 0}{lim}\frac{\Delta y}{\Delta x}\tag6
$$
注意到$u=\frac{\partial y}{\partial t}$,与$(6)$一起带入$(3)$式即得
$$
\frac{\partial^2 \sigma}{\partial x^2}=\frac{1}{E/\rho}\frac{\partial ^2 y}{\partial t^2}\tag7
$$
与波动方程$\frac{\partial^2 \sigma}{\partial x^2}=\frac{1}{u^2}\frac{\partial ^2 y}{\partial t^2}$对比可以得到:
$$
u=\sqrt\frac{E}{\rho}\tag8
$$