七夕佳节,为何不来研究一会数学呢?虽然是昨天的成果,但是现在发出来符合我一贯的作风(手动滑稽
$$
\oint_{\partial S}ud\mathbf{l}=-\iint_{S}{\nabla u\times d\mathbf{S}} \tag{1}
$$
问题的由来
几个月前,还在封闭的宿舍中上着网课。但是这网课吧,它催眠是一级棒的。于是我便在闲暇看看书本,我一行一行地读着那些抽象的文字,我的数理基础受到了严重的考验。就在我跟着例题解算磁偶极子在远程产生的磁场时,一个式子引起了我的注意。
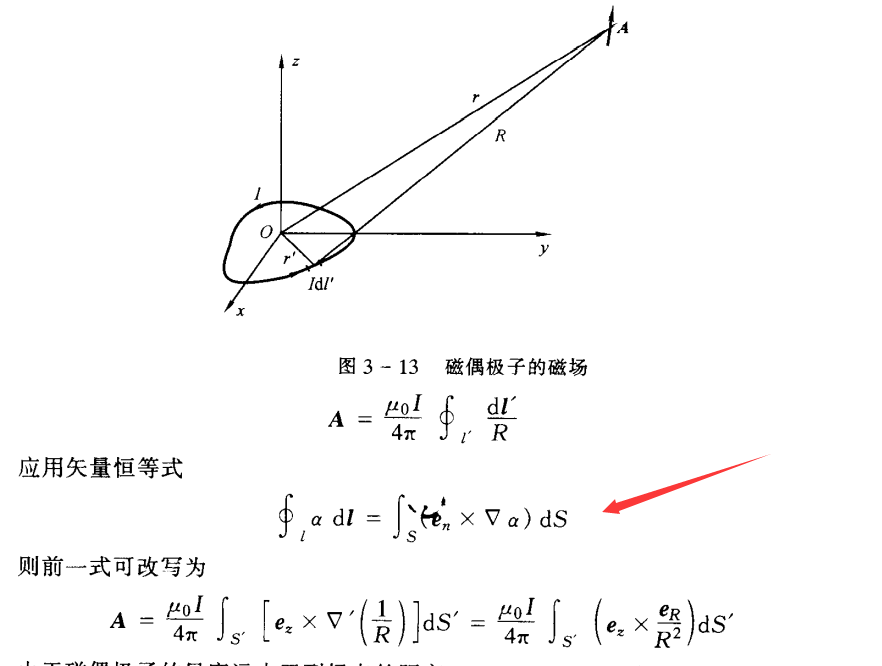
乍一看这与那三大积分定理颇为相似,但是仔细一想,它甚至不是某种通量,因为等式的左右两端都是矢量。一番思考未果,我便去求助于伟大的互联网(Google、Wikipedia、Zhihu、StackExchange),虽然有所发现,但也只是找到了这个式子的另外几种写法,并没有附上证明。后面我又去请教了几位大佬同学,也是没有什么收获,那一个下午便这么过去了。
问题的解决
学期结束,迎来假期,假期摸鱼到如今,掐着手指一算,里开学也就十余天了,我便重起炉灶开始预习。好奇心重,所以翻出了那个式子。在网络搜索方面我重走老路,然而这几个月的时光并没有产生更多关于这个晦涩的式子的信息。
只能说知乎的推荐算法比较厉害,知道我即将复习电磁场(事实上这几天我都在复习《信号与系统》),推荐给了我一篇专栏,在它的最后,我惊喜地发现作者给出了这个公式及其证明,但似乎有一些小小的瑕疵,然后我按照他的思路算了一遍,发现还真可行,于是就有了这篇博文。
证明
一切的铺垫就是为了这一刻的到来,那么我们开始吧
观察(1)式,我们可以发现它的积分结果是一个矢量,要证明两个矢量相等,一个清晰的思路就是证明它们各个分量相等。于是以$x$方向的分量为例:
$$
欲证:(\oint_{\partial S}ud\mathbf{l})\cdot \mathbf{e_x} =-(\iint_{S}{\nabla u\times d\mathbf{S}})\cdot \mathbf{e_x} \tag{2}
$$
我们令$\mathbf{A}=u\mathbf{e_x}$,化简一下(2)式:
$$
只需证:\oint_{\partial S}{\mathbf A \cdot d\mathbf{l}}=\mathbf{e_x}\cdot\iint_{S}{\mathbf{e_n}\times \nabla u dS} \tag{3} \
$$
我们从左边入手:
$$
\begin{align*}
\oint_{\partial S}{\mathbf A \cdot d\mathbf{l}}&=\iint_{S}(\nabla\times \mathbf{A})\cdot \mathbf{e_n}dS \tag4 \\
&=\iint_S{(\frac{\partial u}{\partial z}\mathbf{e_y}-\frac{\partial u}{\partial y}\mathbf{e_z})\cdot \mathbf{e_n}dS} \tag5 \\
&=\iint_S{[\frac{\partial u}{\partial z}(\mathbf{e_n})_y-\frac{\partial u}{\partial y}(\mathbf{e_n})_z]dS} \tag6 \\
&=\mathbf{e_x}\cdot \iint_S{\mathbf{e_n}\times\nabla u dS}\tag7
\end{align*}
$$
于是我们便证明了
$$
(\oint_{\partial S}ud\mathbf{l})\cdot \mathbf{e_x} =-(\iint_{S}{\nabla u\times d\mathbf{S}})\cdot \mathbf{e_x}
$$
对$y,z$方向如法炮制,我们可以得到:
$$
(\oint_{\partial S}ud\mathbf{l})\cdot \mathbf{e_y} =-(\iint_{S}{\nabla u\times d\mathbf{S}})\cdot \mathbf{e_y} \tag8
$$
$$
(\oint_{\partial S}ud\mathbf{l})\cdot \mathbf{e_z} =-(\iint_{S}{\nabla u\times d\mathbf{S}})\cdot \mathbf{e_z} \tag9
$$
于是在$\mathbb{R}^3$中:
$$
\oint_{\partial S}ud\mathbf{l}=-\iint_{S}{\nabla u\times d\mathbf{S}}\quad Q.E.D.
$$
后记
那快感堪比cumming,可惜并非所有人都能有幸体验到。
——知乎网友
就这样吧,祝考试顺利、身体健康!